Lighter, faster, nimbler: Exploring deep learning quantization

The views expressed in this article are solely mine and do not necessarily reflect the views of the my employer.
As deep learning and large language models grow larger, so is the need for more efficient deployment solutions to make them more accessible. This is where quantization comes in — a powerful technique to make deep learning models lighter, faster and nimbler.
Quantization reduces the numerical precision (typically from float to integer[1]) of a model's activations and weights, thereby using less memory and speeding up inference without a substantial loss in accuracy.[2] This opens up a wider range of deep learning use cases, particularly large language models, on everyday hardware.
Whether you're looking to optimize models for edge devices, or simply explore various model optimization techniques, this post will guide you through the basics of quantization, from how it works to strategies of choosing different techniques.
Why quantize your models?
Memory efficiency: A more efficient memory representation means that larger models can be loaded on edge hardware — think your laptop, phone or even IoT devices.
Faster inference speeds: Memory bandwidth is often the bottleneck in deep learning computations , so reducing the number of bits transferred between the CPU and GPU on your device will lead to a speedup. Integer arithmetic is also faster than floating-point arithmetic, as the former manipulates bits directly. With a data-parallel implementation, your inference server can also handle higher throughputs. That said, your mileage may vary.[3]
Reduced carbon intensity: Less computation done means lower energy consumption and the lower associated carbon emissions of deep learning models. This is an increasingly relevant aspect of the model lifecycle as we come to terms on humanity's impact on the environment.
Cost savings: When the application becomes more memory- and compute-efficient, cheaper hardware can be used, leading to cost-savings. Cheaper hardware also unlocks new use cases.
Quantization Basics
To illustrate quantization, let's quantize a tensor from floating-point precision f32, to an 8-bit signed integer i8.

This involves mapping a given range of float values to a target range of integer values.
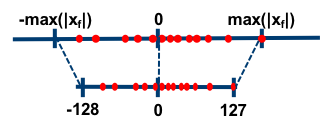
In the example above, we map the range of the largest absolute value to the full range of int8, via a scale parameter.
$$ scale = \frac{\text{abs}(x)}{(2^n-1)} $$
We can then quantize the floats as follows:
$$ q = \text{round}\left(\frac{x}{\text{scale}}\right) $$
Tradeoff between accuracy and memory
Notice that rounding occurs as we convert a float into an integer. This introduces some error when we dequantize the value back to the original data type. In other words, quantization is lossy — error is introduced when rounding the result into an integer datatype. The narrower the quantization type (i4 or i2), the larger the quantization error.
This error propagates through the forward pass during inference, reducing the model's accuracy. Generally, quantizing to int8 does not impact the accuracy too much, justifying the memory savings (~4x). That said, it's prudent that one verifies this for their own use case. Later on, we'll touch upon different quantization techniques one can employ depending on the accuracy degradation.
Above, we gave a simple illustration of how the quantization calculation works. There are other flavours of quantization including:
- symmetric (example above) vs asymmetric quantization
- per-axis vs per-tensor quantization
- quantization mapping function: Linear, quadratic quantization etc
These topics themselves are too much to fit in this post, so feel free to research more on them if you're interested.
Quantization lifecycle of an activation
When an input is fed into a neural network's forward pass, does quantization happen at every layer, or just at the start and at the end? Does it happen at training and at inference?
Quantization is applicable only to inference, with the exception of quantization aware training, as we'll see later.
A model's weights are already quantized. Meanwhile, the input is quantized at the very start. It flows through the network layers and get dequantized at the logit layer. Depending on the implementation, dequantization (and subsequent re-quantization) may also happen in between the layers, depending on whether a layer's operation supports quantization.
Quantization Techniques
There are two broad categories of quantization techniques:
- Post-Training Quantization
- Quantization Aware Training
Post-Training Quantization
These are quantization techniques that can be applied to a trained model — i.e. during inference.
Static Quantization
Weights and activations are statically quantized. This means that the quantization parameters (e.g. scale) are fixed during inference time.
Since the weights of a trained model don't change after training, its quantization parameters are known ahead of time.
However, model activations change with the input. As such, the trained model undergoes a calibration step right before inference. The activations' quantization parameters are estimated based on the activation distribution seen during this step.
How does this work, mechanistically? Observer modules are embedded into the model's layers. In-distribution calibration data is then fed through the network and the observers keep track of the activation distribution statistics—the activations remain unchanged. From this, the quantization parameters for the activations can be estimated.
Since those quantization parameters are fixed, those parameters may not be optimal for all inputs. Thus, static quantization leads can lead to a larger drop in accuracy compared to other quantization techniques. Cue, dynamic quantization.
Dynamic Quantization
Weights are also statically quantized in dynamic quantization. The difference is that the activations are quantized dynamically, wherein the quantization parameters are re-computed for each batch of input.
As the parameters are computed for each batch, the parameters are better suited for the given batch of input, leading to a smaller accuracy drop. However, this approach is slightly slower as the quantization parameters need to be estimated for every batch of input.
Quantization Aware Training
Sometimes, post-training quantization techniques reduce the model accuracy beyond the acceptable threshold for deployment. Quantization aware training is a technique to mitigate this, by modelling the effects of quantization during training itself.
With this technique, fake quantization-dequantization modules are inserted to model (weights and activations) during training.
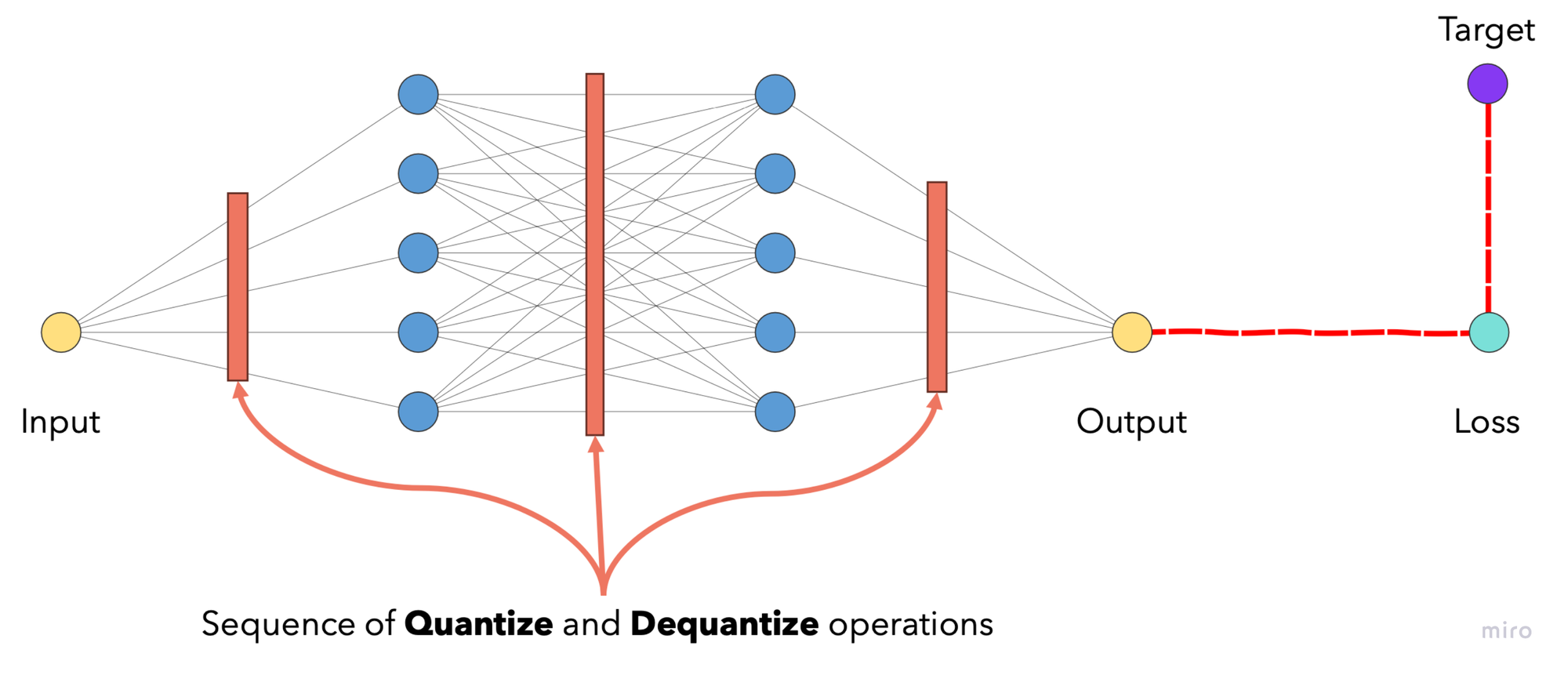
During the forward pass, tensors are quantized and immediately dequantized at these modules, thus taking quantization errors into account when optimizing the loss function. The model's parameters are therefore guided to a point on the loss function where it is robust against quantization errors.
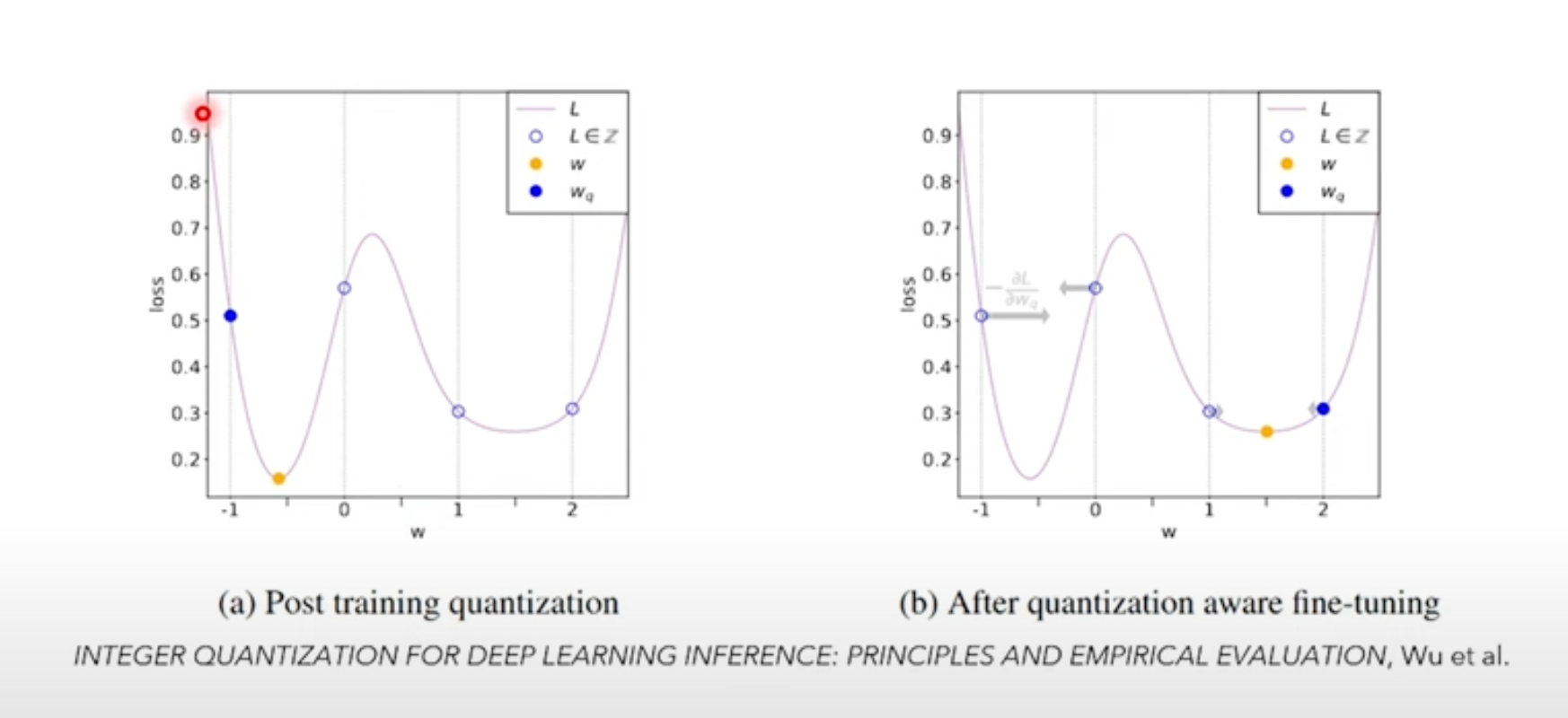
With this technique, you can choose to either fine-tune a model (i.e. train for a few more steps/epochs) or train a new model from scratch.
Summary
Quantization is a powerful optimization tool that unlocks new use cases, for example, by enabling larger models to fit on smaller hardware and/or by reducing the operating costs. When configured properly with the appropriate hardware, it can lead to faster inferences and higher throughputs. And by running less computation overall the carbon intensity of your deep learning application is reduced.
We have seen three approaches for quantization including:
- dynamic quantization
- static quantization
- quantization aware training
The differences between these three techniques can be summarized as follows:
| Technique | Dynamic Quantization | Static Quantization | Quantization Aware Training |
|---|---|---|---|
| Time of application | Post-training | Post-training | Training |
| Weights (during inference) | Statically quantized | Statically quantized | Statically quantized |
| Activations (during inference) | Dynamically quantized | Statically quantized | Statically quantized[4] |
| Weights (during training) | Mixed precision[5] | Mixed precision | Mixed precision + fake quantization |
| Activations (during training) | Mixed precision | Mixed precision | Mixed precision + fake quantization |
| Gradients (during training) | Mixed precision | Mixed precision | Mixed precision |
| Dataset Requirement | None | Calibration set | Fine-tuning set |
| Suitable usage | Transformers; languages; large variation in activations | CNN; vision; fixed, known variation in activations | When either dynamic or static quantization leads to poor accuracy |
When to use each of these techniques
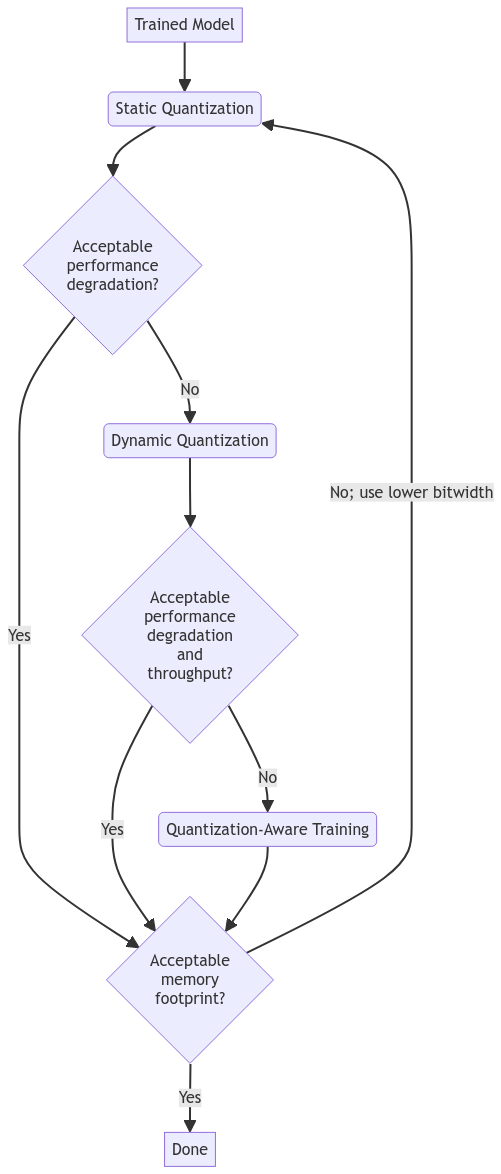
Start with post-training quantization techniques, which are faster and simpler to implement.
Choose static quantization if your application is latency-sensitive, or if your use case's activations typically follow a well-defined range (e.g. vision applications). Otherwise, consider dynamic quantization for improved model accuracies, at the expense of a small increase in inference time.
If model accuracy degrades significantly, fine-tune the original trained model further using quantization aware training.
The workflow can be summarized as follows:
Appendix
More recent advancements
- A Gentle Introduction to 8-bit Matrix Multiplication for transformers at scale using Hugging Face Transformers, Accelerate and bitsandbytes
- Making LLMs Even More Accessible With Bitsandbytes, 4-Bit Quantization and QLoRA
Extra resources on quantization
1. which are discrete values or quanta, hence the technique's name
2. I'm using "accuracy" as a proxy for general machine learning performance metrics (F-beta, MSE, etc.), to disambiguate from engineering performance metrics (latency, memory, etc.)
3. Speed improvement depends on whether the hardware supports the quantized optimizations, and the quantization technique employed. Certain techniques may be slower, as extra quantization and dequantization operations have to be performed.
4. Dynamic quantization is also possible, but is not needed since the model is already quantization-aware
5. Normal (f32) and/or reduced (f16) precision